Zeeman crystals
This experiment follows the working principle of the solid quantum counter, described by Bloembergen [1] and based on an atomic system with 4 energetic levels (Fig. 1 of the IRQC section). For detection of particles in the 10-4eV mass range it further exploits the Zeeman effect.
As suggested by P. Sikivie in 2014 [2], dark matter (DM) axions may induce magnetic dipole transitions between Zeeman-splitted atomic states whose frequency difference, ω, is related to the axion mass, ma, by:
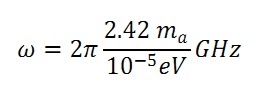
Quantum chromodynamics-based caluclations allows for the ma to be constrained within the 10-6 – 10-3 eV range [3]. However, this sort of axion-atom interaction exhibits an extremely low cross section, such that a mole-sized atomic sample is required to realize a number of axion-driven transitions per second, Ntr, that exceeds at least the unity. Based on this idea, in a previous paper by our group [4], an experiment using a buffer-gas-cooled molecular oxygen sample was proposed for a search at ma≈1.5 meV, corresponding to ω≈2.3 THz.
In this work, in order to further increase Ntr and simultaneously expand down the investigation range for ma, we put into the game a different ordinary-matter specimen, which, represented by a rare-earth-doped crystal, can get to contain a significantly larger number of atoms in a very compact interaction volume. In particular, as a first step towards the implementation of the whole axion DM detection apparatus, an erbium-doped yttrium lithium fluoride (Er3+:LiYF4) crystal is first cryogenically cooled down to a few Kelvins and then subjected to an external magnetic field of ~0.3 T. In such a configuration, laser-induced fluorescence (LIF) spectroscopy is performed to resolve the Zeeman-split ground-state energy levels which determine the axion transition.
Let us denote with Eg- and Eg+, respectively, the energy of the lower (-) and upper (+) sublevel in the Zeeman-split ground state of a T-temperature atomic system subjected to an external magnetic field. After that, let us suppose that kBT << ΔE = Eg+ - Eg-,such that all the atoms occupy (-) sublevel. Then, in the absence of any spurious excitation,(-)→(+) transitions will only be induced as a result of the exposition to the axion field. Atoms promoted to sublevel (+) are eventually detected by LIF spectroscopy by using a laser tuned to some (-)→(e) transition, with "e" indicating a suitable energy level in the visible range, and then observing the fluorescence signal from e. In this scheme, one can scan the ma region of interest by changing the Zeeman splitting via the magnetic field strength (B). Figure 1 shows such transitions for an Er3+:LiYF4 crystal.
A cw Ti-sapphire laser excites the 4I15/2,5/2→4I9/2,9/2 transition (centered at 12361 cm-1) that is followed by a fast (τ ≈ 6 μs) non-radiative decay to the 4I13/2 manifold from where recombination to the ground 4I15/2 takes place and fluorescence (~1.5 μm) is detected (Fig. 2, curve c).
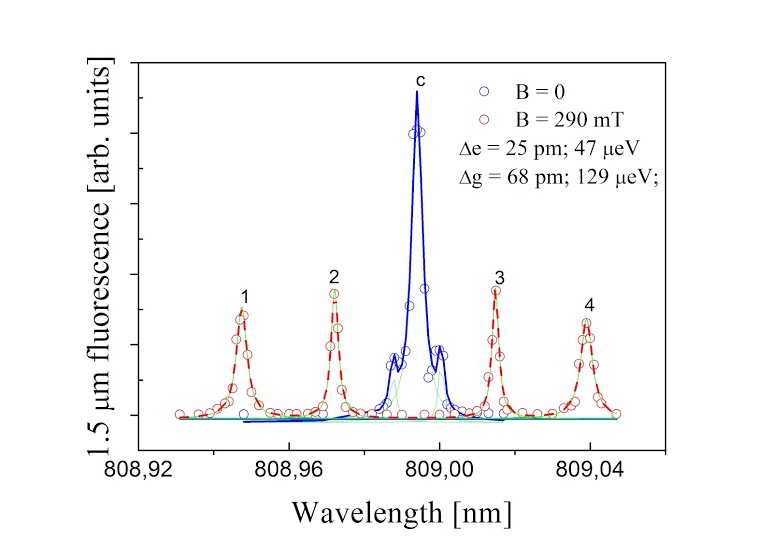
Figure 2 1.5 μm-fluorescence signal of Er3+-doped LiYF4 crystal vs. pumping laser wavelength at 13 K
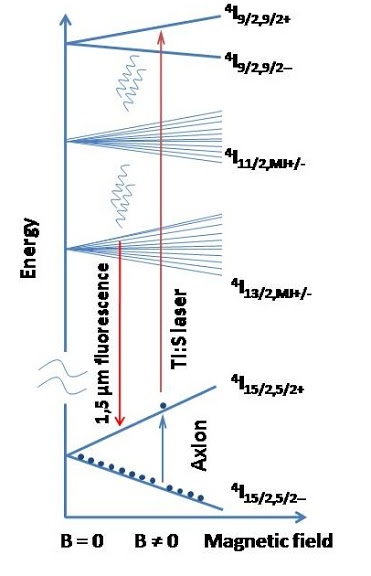
Figure 1 Energetic scheme of the transitions in Er3+-doped LiYF4 crystal
Under the application of magnetic field B~0.3 T, four fluorescence bands are detected. The first one is due to transitions between the 4I15/2,5/2-→4I9/2,9/2+ states, the fourth, corresponding to the lowest energy difference - marks the 4I15/2,5/2+→4I9/2,9/2- transition. The bands 2 and 3 are contributions resulting from the transitions 4I15/2,5/2-→4I9/2,9/2- and 4I15/2,5/2+→4I9/2,9/2+ but cannot be assigned straightforward.
Using what reported in ref. 5, however, we can eventually determine that the Zeeman splitting of the ground state (corresponding to the energy difference between the center of the bands 1 and 3 or 2 and 4, ΔEg) is equal to 129 μeV, while the splitting of the excited 4I9/2,9/2 energy level (the energy difference between the center of the bands 1 and 2 or 3 and 4, ΔEe) is ~47 μeV. We should note that the above described preliminary measurements were conducted at 13 K, where kBT > ΔE. Experiments are in course at liquid helium temperatures and at higher magnetic field, in order to reduce thermal noise and satisfy the condition kBT << ΔE.
References:
- N. Bloembergen, Phys. Rev. Lett. 2 (3) (1959) 84
- P. Sikivie, Phys.Rev. Lett. 113 (2014) 201301
- Borsanyi, S. et al. Nature. 539 (2016) 69–71 doi:10.1038/nature20115 .
- L. Santamaria, C. Braggio, G. Carugno, V. Di Sarno, P. Maddaloni, G. Ruoso, New J. Phys. 17 (2015) 113025, doi:10.1088/1367-2630/17/11/113025
- R. Marino, I. Lorgeré, O. Guillot-Noël, H.Vezin, A. Toncelli, M. Tonelli, J.-L.Le Gouët, P. Goldner, J LUMIN 169 (2016) 478-482