IPHO '99 NEWS
- July, 20, 1999 -
Supplement to the n.3 of "La Fisica nella Scuola"
Managing Director: Luigi Brasini

Italian opera was the theme characterising yesterday's opening ceremony of the XXX International Physics Olympiad taking place in Padua. The notes of Rossini's ingenious Figaro, from Il Barbiere di Siviglia, welcomed the students delegations entering the city "Verdi" Opera Theatre. And the aria "Vincerò" ("I shall win") from Puccini's Turandot accompained their departure after the conclusive official opening of the Olympiad by the President of the Italian Scientific Committee, professor Paolo Violino.
A multicolour assembly was standing yesterday morning at 9 outside the doors of the theatre, waiting for their turn to enter. Students from all over the world occupied the whole small square opposite to the entrance. Some wearing the official uniform of their national team (the Australians also holding a . with the logo of the XXX IphO, the remaining with traditional or simply youth clothing.
Many city and national authorities brought their greetings and wishes to the three hundred students from 62 Countries competing in Padua. Among the others, the Director of the Physics Department at the University of Padua, professor Cesare Voci, recalled the glorious history of physics research, started in Padua four centuries ago by the genius of Galileo, but also the present lively activity of the department he leads. Antonio Cuffaro, representative of the Ministry of scientific research and industry, stressed the responsibility scientists have towards the society and urged the students to think about the key role of scientific research in the development of the world of the future. The representative of the Ministry of education Carla Rocchi and the Rector of the University of Padua Giovanni Marchesini, instead, exhorted the participants to enjoy themselves during this week, dense of competition but also of cultural exchange. A warm welcome from the whole city of Padua was brought by the recently (less than a month ago!) elected Mayor Giustina Mistrello Destro. All of them recognised the Olympiad as a wonderful means of friendship among the peoples of the world.
Francesca Rosati
To study oscillatory motions with on-line apparatuses (sensors + interface + calculator) may be quite exciting. In fact the system evolution in time becomes directly accessible in a quantitative way. Plots of position, velocity and acceleration versus time allow an immediate evaluation of the essential characteristics of the observed motion. Also the experimental investigation within less common graphic representations (velocity/position, acceleration/position, force/acceleration, force/position ...) may offer precious hints for a deeper understanding.

To illustrate the potentialities the on-line experiments, we consider here 3 oscillating systems: two of them being normally part of introductory courses in mechanics (mass-spring and pendulum), while the third (an Atwood machine with one of the masses in water bath) is less common but well suited to show the transition from harmonic to anharmonic behavior, an aspect often neglected in the traditional laboratory.
The mass-spring oscillator (obeying to Hooke's law) is always harmonic, the Atwood oscillator evolves from anharmonic at large amplitude to harmonic at small amplitude (the Archimedes' + gravitational restoring force switches from a constant value to values proportional to displacement when the mass is partially submerged in water) while in the case of pendulum the intrinsically anharmonic motion may be approximated to harmonic motion in the limit of small amplitude.
The position vs. time plots x(t) are quite similar: at first sight they look like sinusoids, more or less damped. However the velocity vs. time plots v(t) show evident differences in the 3 oscillators.
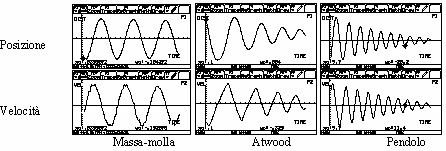
In the mass-spring harmonic oscillator the velocity plot is the same as the position plot, with a phase leading of 90°. In the Atwood oscillator the velocity plot, at large amplitude, is made of straight segments, showing that the motion is uniformly accelerated, with acceleration changing sign at each half-period, while at small amplitude it recall the mass-spring behavior. Also the large amplitude oscillations of the pendulum is far from sinusoidal: you can't see it in the x(t) plot, but you'll see it well in the v(t) plot, and even better in the a(t) plot.
The availability of the whole data set, and not only of few of them (e.g. those related to gate crossing, as in the traditional laboratory) allows this qualitative but important analysis .
Harmonicity implies isochronism. A quantitative analysis of the plots yields immediately the period as a function of amplitude that allows to test the predictions of models for different non-linear restoring forces.
Eight sessions of laboratory demonstrations are scheduled during the Physics Olimpiad in Padua, where many other experiments on oscillations will be performed using a simple on-line apparatus (Galileo oscillator, Maxwell wheel, chart on incline, see-saw on round or square pivot...)
The majority of the phenomena are intrinsically anharmonic motions, as most of the ordinary-life mechanical oscillations. This is due to the fact that usually the restoring force is produced by some component of the gravity field, which is constant. In some cases a quasi harmonic motion may be obtained by choosing a proper system geometry (pendulum) and small departures from equilibrium position. Intrinsically harmonic motion is produced only by a restoring force which is linearly dependent on the displacement, as in the case of mass-spring oscillator, or of the Atwood oscillator (when the immersed body has uniform cross section).
Giacomo Torzo (1) and Barbara Pecori (2)
(1) INFM, CNR and Physics Dept. of Padova University
(2) Physics Dept. of Bologna University
Evangelista Torricelli was among the first experimental physicists to produce vacuum when he invented his barometer to measure atmospheric pressure. In this famous instrument, the upper part of the barometric glass tube was devoid of both air and mercury, and therefore effectively "empty". In fact, it is easy to imagine a process by means of which one can remove all atoms within a certain region to obtain what might be called "classical" vacuum. According to Quantum Mechanics, however, such a vacuum is anything but empty.
To gain an intuitive, albeit partial, view of quantum vacuum one can start from the uncertainty principle which states, among other things, that the energy of a system can be arbitrarily high if it is observed for a very short time (~10-21s): this energy can be sufficient for the creation of particle-antiparticle pairs "filling" the vacuum. A non rigorous picture of the quantum vacuum, as opposed to classical vacuum, is then a sea of continuously forming and annihilating particles. The study of the particles contributing to the structure of vacuum has profound implications besides providing knowledge on the vacuum itself: some of the particles which can appear in the quantum vacuum are almost massless and interact very weakly with radiation and matter, and this makes them good constituents for the still mysterious dark matter filling our universe.
The study of a fundamental physical system such as the quantum vacuum can be approached with the theoretical tools of Quantum Electrodynamics (QED) and with experiments of great beauty and difficulty. The PVLAS experiment investigates the vacuum by perturbing it with a magnetic field and by observing the effects induced on the polarisation state of a light beam used as a probe. In this special case, the external perturbation modifies the optical properties of the vacuum causing it to behave as abirefringent medium. It can be shown that if the probe beam is linearly polarised, it will become elliptically polarised after traversing the vacuum region with a magnetic field (the speed of light in the medium becomes different for different polarisation directions). The characteristic parameters of the polarisation ellipse contain information on physical properties of the vacuum, such as its magnetic and electric permeabilities.
In the PVLAS experiment a linearly polarised laser beam (at 1064 nm) is propagated through the bore of a superconducting, 1 m long, 8 T dipole magnet. The magnet bore is in vacuum and, in order to augment the optical path, the laser light is accumulated for several microseconds in the magnetic field region by means of a Fabry-Perot optical resonator. The total optical path length can thus increase up to 100 km. Nevertheless, the effect to be measured, due to the magnetic birefringence of vacuum, is still quite small: it correspondsto the angle which a 1 Euro coin on the lunar surface subtends on the surface of the earth (about 10-11 rad). Such a small signal can be extracted from the noise background by giving it a known time dependence. This is done in PVLAS by rotating the magnet around a vertical axis: the angle between the magnetic field and the light polarisation direction changes with time, and so does the final effect.

|
|
|
|
Summarising, the PVLAS apparatus consists of:

|
|
|
|
With PVLAS we expect to experimentally determine properties of the vacuum predicted by QED but not yet observed, and to possibly produce and detect in a terrestrial laboratory exotic particles of cosmological interest. The fulfillment of these goals would further strengthen one of the most successful physical theories ever formulated and shed light on some of the great questions that modern cosmology is asking and fundamental physics could answer.
The granite structure is at the center of the picture and is surrounded by scaffolding. Its base rests at the bottom of a square shaped dugout, visible in the picture with railings atound it. The total height of the tower is about 9 m, 7 m from ground level. The top of the granite tower supports an optical bench holding vacuum chambers with part of the optics. A similar optical bench is located in the dugout at the base of the tower. The cryostat housing the magnet is at the center of the tower and is barely visible in the picture: the magnet power supply is the large cabinet at bottom left.
The picture shows a closer view of a portion of the granite tower as seen from ground level. The dark structure is the upper part of the tower and the cilyndrical object inside it is the cryostat. The superconducting magnet is fixed inside the cryostat and the whole assembly (a mass of about 4 tons) can rotate about a vertical axis at a frequency up to 5 Hz.
By INFN National Laboratory of Legnaro